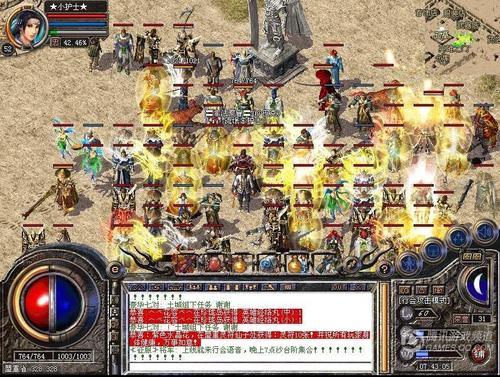
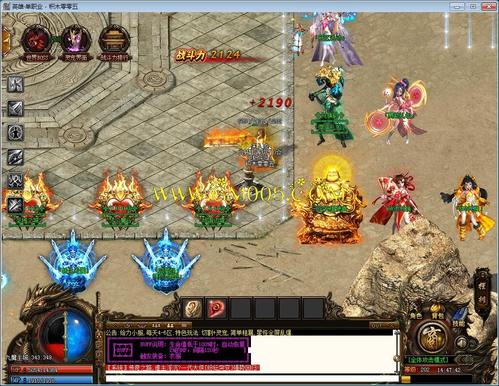
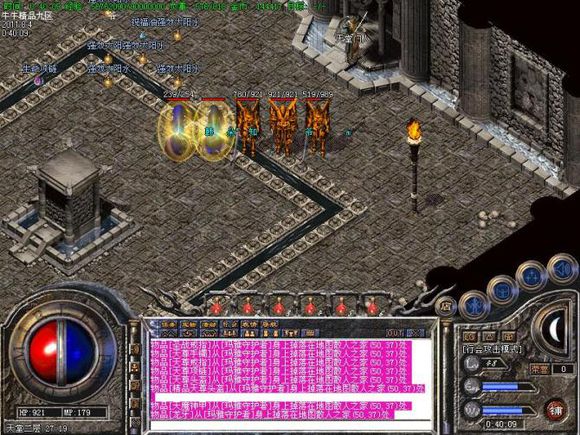
单职业公益:社会责任, 可持续发展, 志愿服务
星期二 2024年9月10日 admin 传奇开服表 单职业公益 0人
传奇无赦单职业:游戏特色、玩法解析与玩家体验
星期一 2024年9月9日 admin 传奇开服表 传奇无赦单职业 0人
谁有好的单职业?深入探讨及建议
星期日 2024年9月8日 admin 传奇开服表 谁有好的单职业 0人
单职业网站: 专注于单职业游戏的平台
星期六 2024年9月7日 admin 传奇开服表 单职业网站 0人
1.80: Understanding the Significance in Mathematics, Finance, and More
星期四 2024年9月5日 admin 传奇开服表 1.80 0人
1.80: Understanding the Significance in Mathematics, Finance, and More
Exploring the Applications of 1.80 in Mathematics
In the realm of mathematics, the number 1.80 serves as a simple yet significant quantity. This decimal not only represents a value but also acts as a key in various calculations and equations. For instance, 1.80 can denote a ratio, where it showcases the relationship between two quantities. In mathematical terms, this ratio could be expressed in fractions, such as 18/10, which simplifies the understanding of proportions. Furthermore, 1.80 is commonly used in statistical analysis, particularly in normal distributions. In such contexts, it can represent standard deviations or z-scores, which are essential for interpreting data sets and making informed decisions based on statistical inference. Therefore, 1.80 is not merely a number but a building block that enhances our understanding of complex mathematical concepts.
Understanding the Significance of 1.95 in Various Contexts
星期三 2024年9月4日 admin 传奇开服表 1.95 0人
Understanding the Significance of 1.95 in Various Contexts
The number 1.95 may seem like a simple numeric value at first glance, but it carries significant implications in various fields such as mathematics, finance, science, and everyday life. Whether you are making calculations, analyzing data, or calibrating measurements, the importance of understanding what 1.95 represents can’t be understated. In this article, we’ll delve into the various contexts where this number appears and explore its relevance, applications, and implications. Lets take a closer look at how 1.95 is utilized and interpreted across different domains.